Die beiden veröffentlichten ihre Ergebnisse in der renommierten Zeitschrift American Mathematical Monthly und erhielten dafür großes Lob und Anerkennung. Diese Leistung, die schon während eines Mathematik-Wettbewerbs an ihrer Highschool begann, bringt neue Perspektiven auf einen der bekanntesten Lehrsätze der Geometrie und inspiriert die Wissenschaft.

Der Satz des Pythagoras: Ein altbekanntes Prinzip neu interpretiert

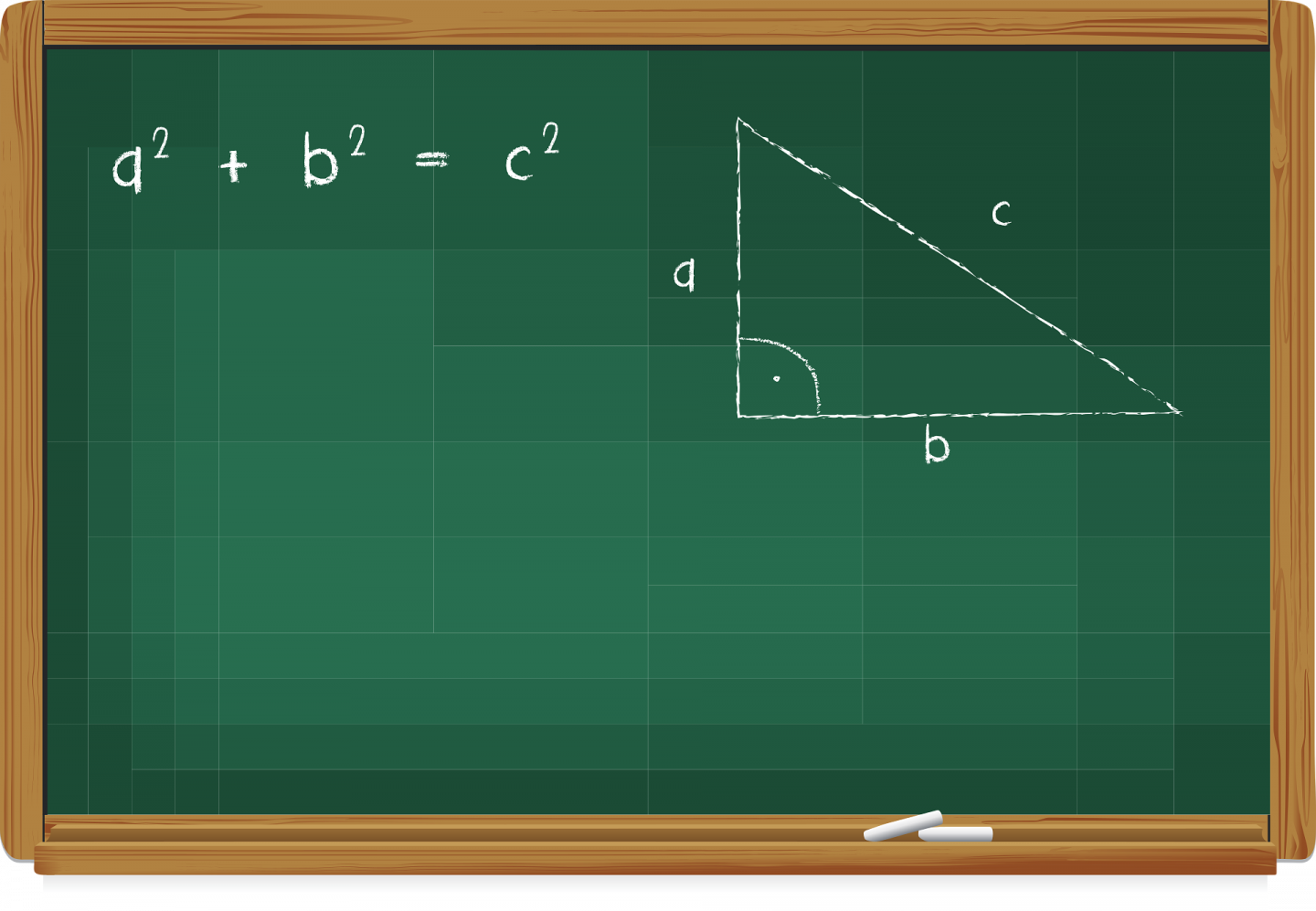
Der Satz des Pythagoras ist eine fundamentale Formel der Geometrie, die besagt, dass die Summe der Quadrate der beiden Katheten eines rechtwinkligen Dreiecks gleich dem Quadrat der Hypotenuse ist. Die Formel, die uns allen als a2+b2=c2a^2 + b^2 = c^2a2+b2=c2 bekannt ist, spielt in der Mathematik und Physik eine zentrale Rolle. Während der Satz durch eine Vielzahl von Methoden bewiesen wurde, gelten trigonometrische Ansätze als besonders knifflig, da Trigonometrie oft selbst auf dem Pythagoras-Prinzip basiert und so potenzielle Zirkelschlüsse entstehen.

Herausforderung Trigonometrie: Vom Highschool-Wettbewerb zur Konferenz

Die beiden Schülerinnen begannen ihre Arbeit im Jahr 2022 als Herausforderung eines Highschool-Wettbewerbs mit einem Preisgeld von 500 Dollar. Was als simple Aufgabe erschien, entwickelte sich schnell zur intensiven Herausforderung: Wochenlang arbeiteten die beiden jungen Frauen bis spät in die Nacht, und sogar in den Ferien an ihren Ideen. Die trigonometrischen Ansätze, die sie entwickelten, ermöglichten es ihnen, mithilfe neuer Konstruktionen von rechtwinkligen Dreiecken verschiedene Beweiswege zu entwickeln. So entstanden fünf verschiedene Herangehensweisen sowie eine Methode zur Generierung weiterer Beweise.

Große Anerkennung und ein Meilenstein für Frauen in der Wissenschaft

Die außergewöhnliche Leistung der beiden Schülerinnen fand breite Anerkennung in der Mathematik-Community. Bei der American Mathematical Society präsentierten sie ihre Arbeit und erregten damit die Aufmerksamkeit von Wissenschaftlern und der Öffentlichkeit. Jackson und Johnson inspirierten viele, insbesondere junge Frauen und Schwarze Frauen, und erhielten zudem lobende Worte von prominenten Unterstützern.

Ein zukunftsweisendes Beispiel: Wissenschaft und Engagement

Heute sind Johnson und Jackson auf dem Weg, in anderen wissenschaftlichen Disziplinen durchzustarten: Johnson studiert Umwelttechnik an der Louisiana State University, während Jackson Pharmazie an der Xavier University of Louisiana studiert. Ihre Entdeckung und ihr Engagement sind ein eindrucksvolles Beispiel für den positiven Einfluss, den junge Talente in der Wissenschaft haben können – und ein Beweis dafür, dass mit Leidenschaft und Durchhaltevermögen selbst scheinbar unlösbare Aufgaben gemeistert werden können.